Il nostro problema è: data una funzione  integrabile
su un intervallo [a,b], calcolare
e se
integrabile
su un intervallo [a,b], calcolare
e se
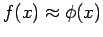 con
con
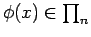 , essendo
l'integrazione di polinomi semplice, il problema viene risolto
calcolando
dove risulta
scegliendo il polinomio interpolante la
, essendo
l'integrazione di polinomi semplice, il problema viene risolto
calcolando
dove risulta
scegliendo il polinomio interpolante la  come
come 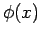 il problema diventa quello di calcolare l'integrale del polinomio
interpolante su determinate ascisse in [a,b].
il problema diventa quello di calcolare l'integrale del polinomio
interpolante su determinate ascisse in [a,b].
Subsections
2004-05-29
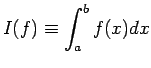
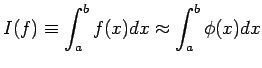
![$\displaystyle \int _a ^ b \phi(x) dx =
\int _a ^b \sum _{i=0} ^n a_i x^i dx =
\left[
\sum _{i=0} ^n a_i \frac{x^{i+1}}{i+1}
\right] _a ^b
$](img438.png)