Formule di quadratura di Newton Cotes

Per adesso consideriamo le ascisse di interpolazione equidistanti quindi $h=(b-a)/n$, $x_i = a+ ih, \: i=0 \ldots n$ quindi $h$ é la distanza tra due ascisse contigue; per i nostri scopi viene utilizzata la base di Lagrange quindi

$$\int _a ^ b p_n(x) dx \equiv \int _a ^ b \sum _{i=0} ^n f_i L_{i\... ... \int _a ^ b \prod _{j=0, j\neq i} ^n \left( \frac{x-x_j}{x_i -x_j} \right) dx$$

dove $\sum _{i=0} ^n f_i$ dipende dalla funziona $f$ ed il resto dipende dalle ascisse di interpolazione (grado del polinomio ed ampiezza dell'intervallo).

$x=a+ih$ con $i$ fissato e discreto, $x=a +th$ con $t$ che varia con continuità su [0,n] e se $t=i$ ottengo $x_i$. Gli estremi di integrazione diventano quindi [0,n] ed il problema viene trasformato nel calcolo di

$$\sum _{i=0} ^ n f_i h \int _0 ^n \prod _{j=0, j \neq i} ^ n \left( \frac{a+th-(a+jh)}{(a+ih)-(a+jh)} \right) dt =$$

$$= h \sum _{i=0} ^ n f_i \left( \int _0 ^n \prod _{j=0, j \neq i} ^ n \frac{t-j}{i-j} dt \right) =I_n(f)$$

$dx=hdt$ e

$$I_n(f) = h \sum _{i=0} ^n \alpha _i ^x f_i$$ (5.1)

e quest'ultima formula prende il nome di formula di quadratura di Newton-Cotes con ascisse equidistanti e le varie $\alpha _i ^n$ sono tabulate nella tabella (5.1) e non dipendono dalla $f$.

Tabella 5.1: I valori sulla riga $i$ vanno divisi per $k[i]$ per ottenere i giusti coefficienti

(n,i)	1	2	3	4	5	6	7	8	k
1	1	1							2
2	1	4	1						6
3	1	3	3	1					8
4	7	32	12	32	7				90
5	19	75	50	50	75	19			288
6	41	216	27	272	27	216	41		840
7	5257	25039	9261	20923	20923	9261	25039	5257	120960

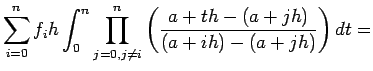
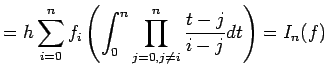
integrale=newtoccotes(f,a,b,m) - Calcola $\int _a ^ b f(x) dx$ mediante la formula di quadratura di Newton Cotes mediante la formula di grado $m$.

%function integrale=newtoncotes(f,a,b,m)
% m=grado della formula di Newton - cotes
% 1 = trapezi
% 2 = Simpson
% 3 = pulcherrima
% 4 = Milne
% 5 =  -
% 6 = Weddle
% 7 = -
% altro = non implementato
function integrale=newtoncotes(f,a,b,m)
newcottab= [ 1 1 0 0 0 0 0 0 ; ...
1 4 1 0 0 0 0 0; ...
1 3 3 1 0 0 0 0 ; ...
7 32 12 32 7 0 0 0 ; ...
19 75 50 50 75 19  0 0 ; ...
41 216 27 272 27 216 41 0 ; ...
5257 25039 9261 20923 20923 9261 25039 5257 ];
ns= [ 2 6 8 90 288 840 120960 ];
n=m+1;

h=(b-a)/m;
x=a:h:b;
F=mfeval(f,x);
integrale=0;
for i=1:n
    integrale=integrale+F(i)*newcottab(m,i);
end
integrale=integrale*(b-a)/ns(m);
return

>> newtoncotes('sin',0,pi,1)

ans =

    1.923607162353882e-016

>> newtoncotes('sin',0,pi,2)

ans =

   2.09439510239320

>> newtoncotes('sin',0,pi,4)

ans =

   1.99857073182384

>> newtoncotes('sin',0,pi,7)

ans =

   2.00001086554154

Specializzando il metodo per $n=1$ ed $n=2$ si ottengono rispettivamente il metodo dei trapezi e quello di Simpson. Nel primo metodo la formula di quadratura diventa

$$I_1(f)=(b-a)/2(f_a + f_b)$$

e corrisponde all'area del trapezio con estremi $(a,0)$ $(b,0)$ $(a,f_a)$ e $(b,f_b)$. Il metodo di Simpson prende invece la seguente forma

$$I_2 (f) = (b-a)/6 (f_a + 4(f\frac{a+b}{2})+ f_b )$$

e corrisponde all'area del settore di parabola che passa per i punti $(a,f_a)$ $(b,f_b)$ e per $(\frac{a+b}{2}, f(\frac{a+b}{2}) )$

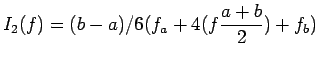
x=trapezi(f,a,b) - Calcola $\int _a ^ b f(x) dx$ mediante il metodo dei trapezi

%TRAPEZI
%function [x]=trapezi(f,a,b)
% Calcola l'integrale di f in [a,b] con la formula 
% dei trapezi.
function [x]=trapezi(f,a,b)
fa=feval(f,a);
fb=feval(f,b);

x=((b-a)/2)*(fa+fb);

return

>> trapezi('sin',0,pi)

ans =

     1.923670693721790e-16

>> type parabola

function y=parabola(x)
y=x^2

>> trapezi ('parabola',0,3)

ans =

  13.50000000000000

x=Simpson(f,a,b) - Calcola $\int _a ^ b f(x) dx$ mediante il metodo di Simpson

%SIMPSON
%function [x]=Simpson(f,a,b)
% Calcola l'integrale di f in [a,b] con la formula 
% di Simpson.
function [x]=Simpson(f,a,b)
fa=feval(f,a);
f1=feval(f,(a+b)/2);
fb=feval(f,b);
x=((b-a)/6)*(fa+4*f1+fb);
return;

>> Simpson('Runge',0,1) 

ans =

   0.78333333333333

>> atan(1)

ans =

   0.78539816339745


>> Simpson('parabola',0,3)

ans =

     9

Ci sono due proprietà fondamentali dei coefficienti $\alpha _i ^n$:

• se $n \leq 7$ allora $\alpha _i ^n \geq 0$
• $1/n \sum _{i=0} ^n \alpha _i ^n = 1 \forall n$