Formule composite di Newton Cotes

Le formule composite di integrazione sfruttano la proprietà di linearità dell'operazione di integrazione ovvero suddividono l'intervallo [a,b] in $n$ intervalli determinati dalle ascisse $a=x_0< x_1 < \ldots < x_n = b$ e calcolano

$$\int _a ^b f(x) dx = \sum _{i=0} ^ n \int _{x_{i-1}} ^{x_i} f(x) dx$$

in questo modo è possibile utilizzare le formule di Newton Cotes fino al settimo grado su intervalli sempre più piccoli soddisfacendo i requisiti di accuratezza e di buon condizionamento del problema.

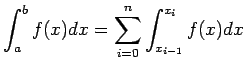
integ=newtoncotescomp(f,a,b,m,n) - Calcola $\int _a ^ b f(x) dx$ mediante le formule compisite di Newton Cotes di grado $m$ su $n$ intervalli

function integ=newtoncotescomp(f,a,b,m,n)
h=(b-a)/n;
x=a:h:b;
integ=0;
for i=1:n-1
    integ=integ+newtoncotes(f,x(i),x(i+1),m);
end
return

>> newtoncotescomp('sin',0,pi,4,100)

ans =

   1.99950656036573

>> newtoncotescomp('sin',0,pi,2,300)

ans =

   1.99994516937386


>> newtoncotescomp('parabola',0,3,4,100)

ans =

   8.73269100000000

>> newtoncotescomp('parabola',0,3,7,100)

ans =

   8.73269100000000

>> newtoncotescomp('parabola',0,3,7,1000)

ans =

   8.97302699100000

Specializzando il metodo si ottengono le formule composite dei trapezi

$$I_{1\:n} (f) \equiv h( \frac{f_0}{2} + f_1 + \ldots+f_{n-1}+ \frac{f_n}{2})$$

x=trapezi-comp(f,a,b,n) - Calcola $\int _a ^ b f(x) dx$ mediante la formula composita dei trapezi con n intervalli

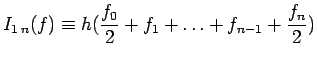
% TRAPEZI-COMP
% function x=trapezi_comp(f,a,b,n)
% Calcola l'integrale di f in [a,b] con la formula 
% composita dei trapezi su n intervalli.
function x=trapezi_comp(f,a,b,n)
h=(b-a)/n;
F=zeros(1,n);
ascisse=a:h:b;
for i=1:n
   F(i)=feval(f,ascisse(i));
end
somma=(F(1)+F(n))/2;
for i=2:n-1
   somma=somma+F(i);
end
x=somma*h;
return

>> type parabola           

function y=parabola(x)
y=x^2;


>> trapezicomp ('parabola',0,3,10)

ans =

   6.60150000000000

>> trapezicomp ('parabola',0,3,15)

ans =

   7.33600000000000

>> trapezicomp ('parabola',0,3,100)


ans =

   8.73313650000000

>> trapezicomp ('parabola',0,3,500)

ans =

   8.94612589199999

e di Simpson (con $n$ pari)

$$I_{2\:n}(f) \equiv h/3 ( f_0 + 4f_1 + 2f_2 + 4f_3 + \ldots + 2f_{n-1} + 4 f_{n-1} + f_n)$$

x=Simpsoncomp(f,a,b,m) - Calcola $\int _a ^ b f(x) dx$ mediante la formula composita di Simpson con $2m+1$ intervalli

%SIMPSONCOMP
% function x=Simpsoncomp(f,a,b,m)
% Calcola l'integrale di f in [a,b] con la formula 
% composita di Simpson su 2m +1 intervalli.
function x=Simpsoncomp(f,a,b,m)
n=2*m+1;
h=(b-a)/n;
F=zeros(1,n);
ascisse=a:h:b;
F=mfeval(f,ascisse);

somma=F(1)+F(n);
for i=2:n-1
   molt=2*(1+(1- mod(i,2)));
   somma=somma+(molt*F(i));
end
x=somma*(h/3);
return

>> type parabola

function y=parabola(x)
y=x^2;


>> Simpsoncomp('parabola',0,3,10)

ans =

    7.7745

>> Simpsoncomp('parabola',0,3,20)

ans =

    8.3574

>> Simpsoncomp('parabola',0,3,100)

ans =

    8.8663

>> Simpsoncomp('parabola',0,3,300)

ans =

    8.9551

>> Simpsoncomp('parabola',0,3,500)

ans =

    8.9731

>> Simpsoncomp('sin',0,pi,10)

ans =

   1.98883637511258

>> Simpsoncomp('sin',0,pi,20)

ans =

   1.99706618390939

>> Simpsoncomp('sin',0,pi,30)

ans =

   1.99867416802724

>> Simpsoncomp('sin',0,pi,100)

ans =

   1.99987785760372