Formule adattative

Le formule composite con ascisse equidistanti sono ottime nel caso in cui la funzione sia abbastanza regolare, ma se la funzione presenta delle regioni in cui cresce velocemente e delle regioni in cui è quasi costante la scelta delle ascisse equidistanti non ottiene buoni risultati, sia per l'accuratezza sia per l'eccessivo numero di calcoli svolti nell' area dove la funzione è quasi costante. Abbiamo quindi bisogno di una ``formula composita variabile'' che si adatti alla forma della funzione aggiungendo più ascisse nella regione in cui la funzione cresce velocemente.

Per fare questo si utilizza una strategia ricorsiva che necessita di una stima dell'errore nel risultato ottenuto per decidere se arrestare l' algoritmo o continuare dividendo in due sotto intervalli l'intervallo di integrazione corrente ed operare ricorsivamente su questi ultimi.

La procedura adaptiv usa come metodo di base quello dei trapezi composito su due intervalli, $I_{1\:2}(f)$. A costo zero è possibile ricavarsi anche il valore di $I_1(f)$. Si può dimostrare che

$$\vert I(f)-I_{1\:2}(f) \vert \approx \frac{1}{3} \vert I_{1\:2}(f)-I_{1}(f) \vert$$

Quindi come criterio di arresto si impone che questa stima dell'errore sia minore di una tolleranza data $\epsilon$. Se la condizione non è verificata si suddivide l'intervallo corrente in due sottointervalli di uguale ampiezza e si richiama ricorsivamente la procedura con tolleranza $\epsilon/2$.

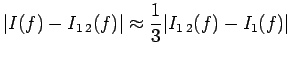
I=adaptiv(f,a,b,tol) - Calcola $\int _a ^ b f(x) dx$ mediante la formula adattativa dei trapezi con tolleranza tol.

%ADAPTIV
%function I=adaptiv(f,a,b,tol)
% Calcola l'integrale di f su [a,b] con 
% tolleranza tol mediante la formula adattativa
% dei trapezi
function I=adaptiv(f,a,b,tol,fa,fb)
if nargin==4
   fa=feval(f,a);
   fb=feval(f,b);
end
h=b-a;
x1=(a+b)/2;
f1=feval(f,x1);
I1=0.5*h*(fa+fb); % metodo dei trapezi
I=0.5*(I1+h*f1); % metodo dei trapezi composito su 2 intervalli
err=abs(I-I1)/3;
 % stima dell'errore
if err>tol
   I=adaptiv(f,a,x1,tol/2,fa,f1)+adaptiv(f,x1,b,tol/2,f1,fb);
end

   

>> adaptiv('sin',0,pi,1E-5)  

ans =

   1.99999307021164

>> adaptiv('Runge',0,1,1E-5) 

ans =

   0.78539745067914

>> atan(1)

ans =

   0.78539816339745