Next: Ricerca dell'autovalore dominante Up: Approssimazione di integrali Previous: Formule adattative Indice
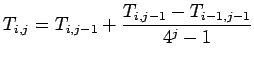
int=romberg(f,a,b,k) -
Calcola
![]() secondo
il metodo di Romberg con k punti di
interpolazione
secondo
il metodo di Romberg con k punti di
interpolazione
%ROMBERG
% function int=romberg(f,a,b,k)
% Calcola l'integrale di f su [a,b] con il metodo di
% estrapolazione di Romberg.
% k e' il numero di valutazioni del metodo dei trapezi che
% devono essere fatte per inizializzare il metodo.
function int=romberg(f,a,b,k)
t=zeros(k,1);
quattro=t;
n=1;
for i=1:k
t(i)=trapezicomp(f,a,b,n);
n=2*n;
end
% Calcola le potenze di quattro in un vettore.
q=4;
for i=1:k
quattro(i)=q;
q=q*4;
end
for i=1:k
for j=k:-1:i+1
t(j)=t(j)+(t(j)-t(j-1))/(quattro(j)-1);
end
end
int=t(k);
>> romberg('sin',0,pi,5)
ans =
1.9747
>> romberg('sin',0,pi,12)
ans =
2.0000
>> romberg('Runge',0,pi,12)
ans =
1.26248605700994
>> atan(pi)
ans =
1.26262725567891
2004-05-29