Il metodo dei minimi quadrati per l'approssimazione polinomiale di funzioni

Il metodo dei minimi quadrati è un metodo numerico per trovare un vettore $x$ che minimizza $\bigr\vert \bigr\vert Ax -b \bigr\vert \bigr\vert _2 ^2$ e può essere applicato all'interpolazione di funzioni mediante polinomi.
Supponiamo di aver effettuato dei campionamenti su un fenomeno mediante $m+1$ coppie $(x_i,f_i)$ e supponiamo che il fenomeno cresca come un polinomio di grado $n$ $(m \gg n)$ il problema è trovare il polinomio $p_n \in \prod _n$ che minimizza le distanze euclidee

$$\sum _{i=0} ^ m ( p_n (x_i) - f_i) ^2$$

dato che $p_n(x)= \sum _{j=0} ^n a_j x^j$ il problema diventa il calcolo del polinomio che minimizza

$$\sum _{i=0} ^ m \left( \sum _{j=0} ^n a_j x _i ^j - f_i \right) ^2$$

per trovare il polinomio non che resta che risolvere il classico sistema di Vandermonde e se tra le $m+1$ ascisse ce ne sono almeno $n+1$ distinte allora la matrice ha rango massimo. Il sistema da risolvere è del tipo $Va=f$ con $V$ matrice di Vandemonde $a$ vettore delle incognite (i coefficienti del polinomio) ed $f$ vettore delle ordinate. La i-esima componente di $Va-f$ è $\sum _{j=0} ^n a_j x _i ^j - f_i$ e quindi $\sum _{i=0} ^ m \left( \sum _{j=0} ^n a_j x _i ^j - f_i \right) ^2 = \bigr\vert \bigr\vert Va - f \bigr\vert \bigr\vert _2 ^2$
Fattorizzando QR la matrice V si ottiene

$$\bigr\vert \bigr\vert Va-f \bigr\vert \bigr\vert _2 ^2 = \bigr\ve... ... \bigr\vert _2 ^2 = \bigr\vert \bigr\vert Ra-Q^T f \bigr\vert \bigr\vert _2 ^2$$

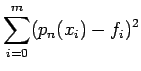
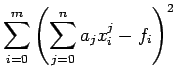
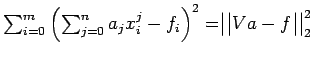
con $R=\left[ \begin{array}{c} R_1 \\ \bigcirc \end{array}\right]$ ; chiamiamo $c=Q^T f =\left[ \begin{array}{c} c_1 \\ c_2 \end{array}\right]$ con $c_1$ di dimensione $n+1$, quindi

$$Ra-c= \left[ \begin{array}{c} R_1 a - c_1 \\ -c_2 \end{arra... ..._2 ^2 + \bigr\vert \bigr\vert c_2 \bigr\vert \bigr\vert _2 ^2$$

e questa è la norma da minimizzare; quindi si pone $a= R_1 ^{-1} c_1$

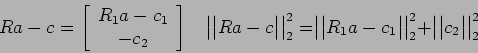
p=MinQuad(x,y,grado) - Trova i coefficienti di un polinomio del grado immesso come parametro, che minimizza le distanze euclidee tra i dati sperimentali (x[i],y[i]) e i valori assunti dal polinomio nelle varie x[i].

%MINQUAD
%function p=MinQuad(x,y,grado)
%
% Calcola il polinomio del grado specificato 
% date le misure sperimentali x e y con il 
% metodo dei minimi quadrati.
function p=MinQuad(x,y,grado)
V=VandermondeRett(x,grado+1);
p=OR(V,y,2);
return

>> x=1:1:10;
>> MinQuad(x,x,1)

ans =

     0     1



>> type parabpert

function y=parabpert(x)
y=3*x^2+2*x+5+sin(x/10);

>> x=1:1:10;
>> y=mfeval('parabpert',x)

y =

   10.0998
   21.1987
   38.2955
   61.3894
   90.4794
  125.5646
  166.6442
  213.7174
  266.7833
  325.8415

>> MinQuad(x,y,2)

ans =

    5.0033    2.1035    2.9982


>> polyfit(x,y,2)

ans =

    2.9974    2.1114    4.9873

La procedura descritta sopra utilizza due procedure ausiliarie:

• VandermondeRett per riempire la matrice di Vandermonde
• OR per trovare il vettore di minima norma attraverso la fattorizzazione QR

Figura 4.1: Applicazione del metodo dei minimi quadrati a dati sperimentali che crescono linearmente

Figura 4.2: Applicazione del metodo dei minimi quadrati a dati sperimentali con andamento quadratico