Next: Formule composite Up: Accuratezza ed errore Previous: Condizionamento del problema Indice
![$\displaystyle I(f) - I_n(f) = \int _a ^b ( f(x) -p_n(x)) dx = \int _a ^b
f[x_0, \ldots, x_n,x] \omega _{n+1}(x) =
$](img483.png)
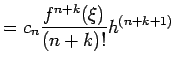
Il problema è che
![]() deve andare a 0, ma se
deve andare a 0, ma se ![]() cresce il problema diventa
mal condizionamento; per far andare
cresce il problema diventa
mal condizionamento; per far andare ![]() a 0 allora si lascia
a 0 allora si lascia ![]() invariato e si fa tendere
invariato e si fa tendere
![]() a 0 e questa è la base delle formule composite di Newton Cotes.
a 0 e questa è la base delle formule composite di Newton Cotes.