ovviamente A è triangolare inferiore e vale la seguente
condizione
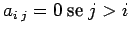 ; per le triangolari
superiori vale invece
; per le triangolari
superiori vale invece
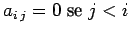 . In
entrambi i casi
. In
entrambi i casi
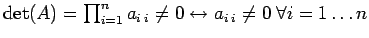 .
Nel caso delle triangolari inferiori l'equazione i-esima è
.
Nel caso delle triangolari inferiori l'equazione i-esima è
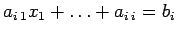 con
con
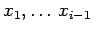 determinate ai
passi precedenti; nell'altro caso l'equazione i-esima è
determinate ai
passi precedenti; nell'altro caso l'equazione i-esima è
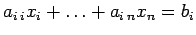 con
con
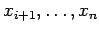 determinati
precedentemente. In entrambi i casi il costo dell'algoritmo è quadratico.
determinati
precedentemente. In entrambi i casi il costo dell'algoritmo è quadratico.
2004-05-29
