Metodo di Neville per il calcolo del polinomio interpolante in un punto

Se ci interessa il valore del polinomio interpolante in un solo punto si può usare l'algoritmo di Neville che opera in modo simile al calcolo delle differenze divise e si basa sulla seguente formula

$$P_i(x) \equiv f_i$$

$$P_{i \: i+1 \ldots j}(x)=\frac{P_{i \: i+1 \ldots j-1}(x) (x-x_j) - P_{ i+1 \ldots j}(x)(x-x_i)}{x_i-x_j}$$

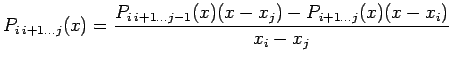y0=Neville(x0,x,f) - Applica il metodo di Neville per trovare il valore del polinomio interpolante le ascisse x e le ordinate f nel punto x0

%NEVILLE
% function y0=Neville(x0,x,f)
%
% Calcola il valore del polinomio interpolante la f sulle
% ascisse x nel punto x0 secondo lo schema di Neville.
% See also INTERPOLA, HORNER, CEBYSHEV
function y0=Neville(x0,x,f)
n=length(x); 

for i=1:n
    for j=n:-1:i+1
	f(j)= f(j) + ( f(j) - f(j-1) ) ...
	 *(x0 - x(j))/( x(j) - x(j-i));
    end
end
y0=f(n);
return

>> x=Cebyshev(0,5,5)

x =

   4.87764129073788   3.96946313073118   
   2.50000000000000   1.03053686926882
   0.12235870926212

>> f=mfeval('exp',x)

f =

   1.0e+02 *

   1.31320551296239
   0.52956092707808
   0.12182493960703
   0.02802570044612
   0.01130159427733

>> x0=Neville(1,x,f)

x0 =

   2.67288785979018

>> exp(1)

ans =

   2.71828182845905