Next: Neville Up: Interpolazione di funzioni Previous: Ascisse di Cebyshev Indice
Gli elementi della base di Lagrange sono così definiti:
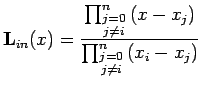 |
(3.3) |
Osserviamo anche che
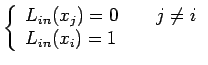
Vogliamo ora trovare i coefficienti del polinomio interpolante nella base di Lagrange
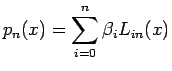
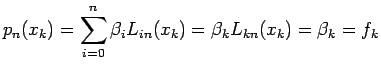
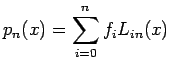
Questo risultato è importante dal punto di vista implementativo: i
coefficienti del polinomio interpolante sono noti, essendo gli ![]() i
dati del problema, l'algoritmo quindi deve solo calcolare il valore dei
polinomi di base nelle ascisse di tabulazione.
i
dati del problema, l'algoritmo quindi deve solo calcolare il valore dei
polinomi di base nelle ascisse di tabulazione.
In particolare la procedura LagrangeInterpola costruisce una
matrice ![]() che ha
che ha ![]() righe (dove
righe (dove ![]() è il grado del polinomio
interpolante) e
è il grado del polinomio
interpolante) e ![]() colonne dove con
colonne dove con ![]() indichiamo il numero
di punti di tabulazione; questa matrice contiene nella posizione
indichiamo il numero
di punti di tabulazione; questa matrice contiene nella posizione
![]() il valore di
il valore di
![]() nell'ascissa di tabulazione
di posizione
nell'ascissa di tabulazione
di posizione ![]() .
In simboli se indichiamo con
.
In simboli se indichiamo con ![]() il vettore che contiene i punti di
tabulazione e con
il vettore che contiene i punti di
tabulazione e con ![]() l'elemento di posto
l'elemento di posto ![]() della
matrice
della
matrice ![]() si ha
si ha
![]() e
e
Una volta costruita questa matrice, i valori assunti dal polinomio
interpolante nelle ascisse di tabulazione si ottengono facilmente dal
prodotto del vettore che contiene gli ![]() e la matrice
e la matrice ![]() . Infatti
. Infatti
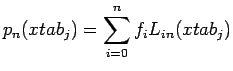
La procedura LagrangeInterpola riceve una funzione da
interpolare, il vettore delle ascisse di interpolazione e il numero di
punti di tabulazione da calcolare.
La matrice ![]() è ottenuta richiamando la procedura ausilaria
Lag che calcola in parallelo il valore del nominatore dei vari
è ottenuta richiamando la procedura ausilaria
Lag che calcola in parallelo il valore del nominatore dei vari
![]() nelle ascisse di tabulazione e poi dividendo tutti i suoi
elementi per il valore del denominatore che dipende solo dalle ascisse
si interpolazione e non dal punto in cui deve essere calcolato
nelle ascisse di tabulazione e poi dividendo tutti i suoi
elementi per il valore del denominatore che dipende solo dalle ascisse
si interpolazione e non dal punto in cui deve essere calcolato
![]() (questi calcoli sono svolti dalla procedura
lag_denom).
(questi calcoli sono svolti dalla procedura
lag_denom).
I valori del polinomio nei punti di tabulazione sono ottenuti dal
prodotto del vettore ![]() (che contiene gli
(che contiene gli ![]() ) per la
matrice
) per la
matrice ![]() .
.
Dato che il polinomio di grado ![]() interpolante una funzione è
unico, anche se i calcoli effettuati sono diversi, la procedura
LagrangeInterpola trova gli stessi valori della procedura
Interpola.
interpolante una funzione è
unico, anche se i calcoli effettuati sono diversi, la procedura
LagrangeInterpola trova gli stessi valori della procedura
Interpola.
Valgono perciò le considerazioni esposte nel paragrafo
3.4 e quindi è conveniente passare anche a questa
procedura un vettore ![]() contenente le ascisse di Cebyshev.
contenente le ascisse di Cebyshev.
2004-05-29