Metodo delle corde

Se ci troviamo abbastanza vicino alla soluzione $\overline{x}$ allora la pendenza della retta tangente il grafico della funzione non cambia di molto e quindi $f^{\prime}$ ci dice in qualche modo in che direzione dobbiamo guardare per trovare la soluzione. Quindi il metodo delle corde, calcola $f^{\prime}(x_0)$ e lascia invariato questo valore usandolo al posto di $f^{\prime}(x_i)\quad i=1\ldots$. Quindi il metodo diventa

$$x_{n+1}= x_n - \frac{f(x_n)}{f^{\prime}(x_0)}$$

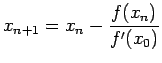
La funzione ha comunque bisogno di conoscere $f$ e $f^{\prime}$. La valutazione di $f^{\prime}$ avverrà solo al primo passo.

Il costo del metodo delle corde è assimilabile a quello di bisezione perché ad ogni passo l'operazione predominante è una valutazione della $f$; il metodo è convergente di ordine 1, comunque scegliendo il punto di innesco adeguatamente si ottiene una convergenza più veloce. Nell'esempio tuttavia osserviamo che il metodo delle corde impiega 1978 iterazioni a trovare la radice della funzione $y=e^x-1$ partendo da $x_0=4$ contro i 10 passi del metodo di Newton.

[$x$,passi]=corde(f,df,x0,epsilon,upper) - Applica il metodo delle corde alla funzione $f$ (la cui derivata è df) con punto iniziale $x_{0}$, accuratezza epsilon e numero massimo di passi upper. Restituisce in $x$ la radice (se trovata) e in passi, il numero di passi effettuati.

%CORDE
%[x,passi]=corde(f,df,x0,epsilon,upper)
%  Pre: f derivabile
%  Applica il metodo delle corde per il calcolo della
%  radice dell'equazione f(x)=0
%  f       - funzione
%  df      - derivata di f
%  x0      - punto di innesco
%  epsilon - tolleranza per la radice
%  upper   - numero massimo di iterazioni consentite 
%
%  Restituisce in x la radice trovata e in passi il numero
%  di iterazioni che sono state necessarie per reggiungerla
%  See also BISEZ,  NEWTON, SECANTI.
function [x,passi]=corde(f,df,x0,epsilon,upper)
count=0;
d=feval(df,x0);
while(count<upper) & (abs(feval(f,x0))>epsilon)
   count=count+1;
	x0=x0-(feval(f,x0)/d);
end
x=x0;
passi=count;
return

>> type f_e

function y=f_e(x)
y=exp(x)-1;

>> [x,passi]=corde('f_e','exp',4,1E-19,10000)

x =

    1.097812158372279e-016


passi =

        1978

Nella figura 2.2 vediamo il grafico che illustra il comportamento del metodo delle corde applicato alla funzione $y=e^{x}-1$ con punto di partenza $x=2$. In questo caso il metodo ha bisogno di ben 250 iterazioni per convergere alla soluzione con un errore dell'ordine di $10^{-17}$.

Figura 2.2: Metodo delle corde applicato alla funzione $y=e^x-1$ con punto di partenza $x_0=2$. Converge alla radice $\overline{x}=0$ in 250 passi.