Next: Interpolazione di funzioni Up: Equazioni non lineari Previous: Metodo delle corde Indice
Il metodo delle secanti è un ``ibrido'' tra il metodo di Newton ordinario
e quello delle corde, poiché ad ogni passo né calcola la derivata prima
della funzione, né tiene fissato un valore, ma approssima la derivata
con la pendenza della retta secante il grafico della funzione passante per le
due approssimazioni precedenti.
In pratica ![]() viene calcolato con il metodo di Newton ordinario e successivamente il metodo
diventa del tipo
viene calcolato con il metodo di Newton ordinario e successivamente il metodo
diventa del tipo
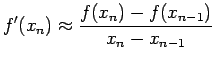
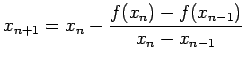
[![]() ,passi]=secanti(f,df,x0,epsilon,upper) -
Applica il
metodo delle secanti alla funzione
,passi]=secanti(f,df,x0,epsilon,upper) -
Applica il
metodo delle secanti alla funzione ![]() (con derivata
(con derivata ![]() ) con punto iniziale
) con punto iniziale ![]() ,
accuratezza epsilon e numero massimo di passi upper. Restituisce in
,
accuratezza epsilon e numero massimo di passi upper. Restituisce in
![]() la radice (se trovata) e in passi, il numero di passi effettuati.
la radice (se trovata) e in passi, il numero di passi effettuati.
%SECANTI %[x,passi]=secanti(f,x0,epsilon,upper) % Pre: f derivabile % Applica il metodo delle secanti per il calcolo della % radice dell'equazione f(x)=0 % f - funzione % x0 - punto di innesco % epsilon - tolleranza per la radice % upper - numero massimo di iterazioni consentite % % Restituisce in x la radice trovata e in passi il numero % di iterazioni che sono state necessarie per reggiungerla % See also BISEZ, NEWTON, CORDE. function [x,passi]=secanti(f,df,x0,epsilon,upper) count=0; x_old=x0; y_old=feval(f,x_old); d=feval(df,x0); x_curr=x0-y_old/d; y_curr=feval(f,x_curr); while(count<upper) & (abs(y_curr)>epsilon) count=count+1; tmp_x=x_curr; tmp_y=y_curr; x_curr=tmp_x -((tmp_y*(tmp_x - x_old))/(tmp_y -y_old)); y_curr=feval(f,x_curr); x_old=tmp_x; y_old=tmp_y; end x=x_curr; passi=count; return
>> type f_e
function y=f_e(x)
y=exp(x)-1;
>> [x,passi]=secanti('f_e','exp',4,1E-19,300)
x =
1.230367509482608e-017
passi =
13
Nel grafico di figura 2.3 è illustrato il
comportamento del metodo delle secanti applicato alla funzione
![]() con punto di innesco
con punto di innesco ![]() . Il metodo converge alla radice
con un errore dell'ordine di
. Il metodo converge alla radice
con un errore dell'ordine di ![]() in 10 passi.
Nella figura è disegnata in colore verde la retta tangente in
in 10 passi.
Nella figura è disegnata in colore verde la retta tangente in ![]() ottenuta dal metodo di Newton ordinario.
ottenuta dal metodo di Newton ordinario.
2004-05-29