Metodo di accelerazione di Aitken

Questo metodo serve per ripristinare la convergenza quadratica del metodo di Newton nel caso di radici multiple con molteplicitá sconosciuta; nel caso di molteplicità nota $r$ si deve utilizzare questa variante del metodo precedente

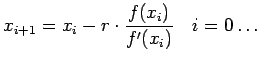$$x_{i+1}=x_{i} - r\cdot \frac{f(x_{i})}{f^{\prime}(x_{i})} \quad i=0\ldots$$ (2.6)

Si può ossevare che questo metodo converge in una sola iterata se la funzione è del tipo $y=\alpha(x-\overline{x})^r$, infatti

$$x_{n+1}=x_n-\frac{r \alpha (x_n-\overline{x})^r}{r\alpha(x_n-\overline{x})^{r+1}}=x_n-x_x+\overline{x}=\overline{x}$$

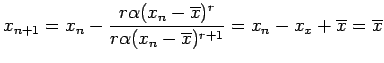
[x,passi]=Newtonmolt(f,df,x0,r,epsilon,upper) - Applica il metodo di Newton alla funzione $f$, la cui derivata è $df$, con punto iniziale $x_{0}$, molteplicità della radice r accuratezza epsilon e numero massimo di passi upper. Restituisce in $x$ la radice (se trovata) e in passi, il numero di passi effettuati.

%NEWTONMOLT
%[x,passi]=Newtonmolt(f,df,x0,r,epsilon,upper)
%  Pre: f derivabile
%  Applica il metodo di Newton per il calcolo della
%  radice (di molteplicita' nota r) dell'equazione f(x)=0 
%  f       - funzione
%  df      - derivata prima di f
%  x0      - punto di innesco
%  r       - molteplicita' della radice
%  epsilon - tolleranza per la radice
%  upper   - numero massimo di iterazioni consentite 
%
%  Restituisce in x la radice trovata e in passi il numero
%  di iterazioni che sono state necessarie per reggiungerla
%  See also BISEZ,  CORDE, SECANTI.

function [x,passi]=Newtonmolt(f,df,x0,r,epsilon,upper)
count=0;
f0=feval(f,x0);
d=feval(df,x0);

while(count<upper) & (abs(f0)>abs(epsilon*d))
	count=count+1;
	d=feval(df,x0);
    x0=x0-r*(f0/d);
    f0=feval(f,x0);   
end
x=x0;
passi=count;
return

function y=fm(x)
y=(x-5)^5;

>> type dfm

function y=dfm(x)
y=5*(x-5)^4;

>> [x,passi]=Newton('fm','dfm',6,1E-5,200)

x =

   5.00010633823966


passi =

    41

>> [x,passi]=Newtonmolt('fm','dfm',6,5,1E-5,200)

x =

     5


passi =

     1

Il metodo di accelerazione di Aitken, invece, utilizza questa approssimazione per l'approssimazione $\overline{x_n}$, note due approssimazioni precedenti che convergono linearmente, $x_{n-1}$ e $x_{n-2}$:

$$\overline{x_n} \approx \frac{x_n^2-x_{n-1}x_{n+1}}{2x_n-x_{n+1}-x_{n-1}}$$ (2.7)

In pratica il metodo di accelerazione si utilizza nel seguente modo:

• Si parte con $x_0$ e si generano $x_1$ e $x_2$ con il metodo di Newton.
• Con questi 3 punti si puó costruire $\overline{x_1}$ sfruttando la formula (2.7).
• Si pone $x_0= \overline{x_1}$ e si generano $x_1$ e $x_2$
• Con questi nuovi valori si può costruire l'ulteriore approssimazione $\overline{x_2}$.
• Il procedimento si ripete iterativamente.

Come si vede dall'esempio, questo metodo è molto efficace nel caso di radici multiple. Applicandolo alla funzione $y=(x-5)^4$ trova la radice con una accuratezza pari a $10^{-14}$ in 3 passi contro i 134 del metodo di Newton.

[$x$,passi]=Aitken(f,df,x0,epsilon,upper) - Applica il metodo di Newton con accelerazione di Aitken alla funzione $f$ (la cui derivata è $df$) con punto iniziale $x_{0}$, accuratezza epsilon e numero massimo di passi upper. Restituisce in $x$ la radice (se trovata) e in passi, il numero di passi effettuati.

%AITKEN
%function [x,passi]=Aitken(f,df,x0,epsilon,upper)
%
% Trova la radice della funzione f con derivata df 
% applicando il metodo di accelerazione di Aitken 
% con punto iniziale x0, tolleranza epsilon e numero
% massimo di passi upper.
% Restituisce in x il valore della radice e in passi
% il numero di iterazioni eseguite.
function [x,passi]=Aitken(f,df,x0,epsilon,upper)

f0=feval(f,x0);
d=feval(df,x0);
x1=x0-(f0/d);
f1=feval(f,x1);   

d=feval(df,x1);
x2=x1-(f1/d);
f2=feval(f,x2);

count=0;

while (count<upper) & abs(f2)>abs(epsilon*d)
   count=count+1;
   x0=(x1*x1-x0*x2)/(2*x1-x2-x0);
   f0=feval(f,x0);
   d=feval(df,x0);
   x1=x0-(f0/d);
   f1=feval(f,x1);   
   d=feval(df,x1);
   x2=x1-(f1/d);
   f2=feval(f,x2);      
end
x=x2;
passi=count+2;
return

>> type fm

y=(x-5)^5;

>> type dfm

function y=dfm(x)
y=5*(x-5)^4;

>> [x,passi]=Newton('fm','dfm',6,1E-14,300)

x =

   5.00000000000010


passi =

   134

>> [x,passi]=Aitken('fm','dfm',6,1E-14,300)

x =

   4.99999999999993


passi =

     3