Per trovare i coefficienti del
polinomio basta risolvere un sistema lineare del tipo:
la matrice contenente le 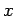 prende il nome di matrice di
Vandermonde ed il numero di
condizionamento associato alla matrice cresce
più che esponenzialmente in
prende il nome di matrice di
Vandermonde ed il numero di
condizionamento associato alla matrice cresce
più che esponenzialmente in  ,
quindi si cerca un approccio diverso alla risoluzione del problema.
La costruzione di questa matrice ci permette comunque di concludere che
tale polinomio interpolanate è unico perché la matrice è
non singolare in quanto il suo determinante è
,
quindi si cerca un approccio diverso alla risoluzione del problema.
La costruzione di questa matrice ci permette comunque di concludere che
tale polinomio interpolanate è unico perché la matrice è
non singolare in quanto il suo determinante è
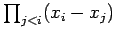 e noi abbiamo supposto che le varie
e noi abbiamo supposto che le varie  distinte.
distinte.
La procedura VanderInterp trova i coefficienti del polinomio
costruendosi la matrice di Vandermonde 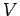 e risolvendo il sistema
lineare
e risolvendo il sistema
lineare 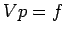 . Tuttavia questo metodo dà luogo ad un sistema
mal condizionato e pertanto la procedura VanderInterp non dà
risultati attendibili.
. Tuttavia questo metodo dà luogo ad un sistema
mal condizionato e pertanto la procedura VanderInterp non dà
risultati attendibili.
2004-05-29
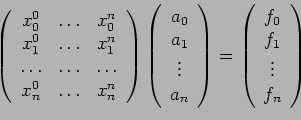
![]() e risolvendo il sistema
lineare
e risolvendo il sistema
lineare ![]() . Tuttavia questo metodo dà luogo ad un sistema
mal condizionato e pertanto la procedura VanderInterp non dà
risultati attendibili.
. Tuttavia questo metodo dà luogo ad un sistema
mal condizionato e pertanto la procedura VanderInterp non dà
risultati attendibili.