Metodo di bisezione

Supponiamo che $f$ sia una funzione continua nell'intervallo $[a,b]$ tale che $f(a)f(b)<0$ cioè la funzione assume valori di segno opposto nei due estremi. Allora per il teorema dell'esistenza degli zeri $\exists c : a < c < b, f(c)=0$.

Definiamo $x_{1}=\frac{a+b}{2}$ allora si può avere uno dei seguenti tre casi:

1. $f(x_{1})=0$ allora abbiamo avuto fortuna: $x_{1}$ è una radice e l'algoritmo termina.
2. $f(a)f(x_{1})<0$ allora possiamo reiterare il procedimento sul nuovo intervallo $[a,x_{1}]$.
3. $f(b)f(x_{1})<0$ allora possiamo reiterare il procedimento sul nuovo intervallo $[x_{1},b]$.

In un passo abbiamo in questo modo dimezzato l'ampiezza dell'intervallo di confidenza, quindi reiterando questo metodo è possibile trovare un intervallo di confidenza di ampiezza sempre più piccola.

Poiché $x_{1}=\frac{a+b}{2}$ si ha $\vert\overline{x}-x_{1}\vert<\frac{b-a}{2}$. In generale $\vert\overline{x}-x_{i}\vert<\frac{b_{i}-a_{i}}{2}$. Sviluppando questa relazione si ottiene

$$\vert\overline{x}-x_{i}\vert<\frac{b-a}{2^{i}} \leq \epsilon$$

$$b-a \leq \epsilon 2^{i}$$

$$\frac{b-a}{\epsilon} \leq 2^{i}$$

$$\log_{2}{(b-a)}-\log_{2}{(\epsilon)} \leq i$$

$$i \geq \lceil \log_{2}{(b-a)}-\log_{2}{(\epsilon)} \rceil = \nu$$ (2.1)

In questo modo, fissata la accuratezza $\epsilon$, viene fissato anche il numero massimo di iterazioni, $\nu$. Nella nostra implementazione, epsilon viene dato dall'utente e $\nu$ viene calcolato secondo la formula (2.1) e restituito in nu.

Un altro problema che si presenta nell'implementazione dell'algoritmo è la condizione $f(x_{i})=0$ che è difficilmente verificabile in aritmetica finita e dev'essere più realisticamente sostituita con una condizione del tipo $\vert f(x_{i})\vert<\delta$ dove $\delta$ soddisfa

$$\delta=\delta(\epsilon) \textrm{ tale che } \vert f(x_i)\vert<\delta \Longrightarrow \vert\overline{x}-x_{i}\vert<\epsilon$$ (2.2)

Tale $\delta$ risulta essere

$$\delta \approx \epsilon \vert f'(x_{i})\vert$$ (2.3)

Tuttavia calcolare esplicitamente $f'(x_{i})$ sarebbe più costoso del metodo di bisezione stesso. Quello che possiamo fare è approssimare $f'(x_{i})$ con il rapporto incrementale che ha come estremi l'intervallo corrente $[a_{i},b_{i}]$:

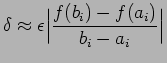$$\delta \approx \epsilon \Big\vert\frac{f(b_{i})-f(a_{i})}{b_{i}-a_{i}}\Big\vert$$ (2.4)

Nell'esempio vediamo l'applicazione della procedura di bisezione alla funzione $y=\sin(x)$. L'intervallo di confidenza iniziale è $[2; 4]$ (osserviamo che la funzione assume valori di segno opposto. In questo caso il metodo converge alla soluzione $\overline{x}=\pi$ in 49 passi mentre il limite fissato con la formula (2.1) è 51. La funzione $\sin$ è molto regolare quindi si ha $\delta=\epsilon$.

Nel caso che la radice non sia semplice e quindi la funzione sia molto schiacciata (nell'esempio $y=(x-5)^5$) ad un $\epsilon$ piccolo corrisponde un $\delta$ abbastanza grande: nell'esempio ad $\epsilon=10^{-5}$ corrisponde un $\delta$ dell'ordine di $10^{-1}$.

[$x$,nu,delta,passi]=bisez(f,a,b,epsilon) - Applica il metodo di bisezione alla funzione $f$ nell'intervallo [a,b] con accuratezza epsilon; precondizioni> $f$ continua in [a,b] e $f(a)\cdot f(b)<0$. Restituisce in $x$ la radice trovata, in nu il limite superiore al numero di passi da eseguire, in delta l'accuratezza sulle $y$ in $passi$ il numero di passi effettuati.

%BISEZ
%[x,nu,delta,i]=bisez(f,a,b,epsilon)
%dove 
%- f e' il NOME di una funzione f
%- a e b sono gli estremi di un intervallo tale che f(a)*f(b)<0
%- epsilon e' l'accuratezza desiderata
%
% applica il metodo di bisezione e restituisce in x una radice
% di f(x)
% In nu viene resttituito il limite superiore 
% al numero di iterazioni affinche'
% il metodo sia attendibile con
% accuratezza epsilon; in delta viene restituita
% l'accuratezza sulle y 
% See also NEWTON
function [x,nu,delta,i]=Bisez(f,a,b,epsilon)
nu=ceil(log2(b-a)-log2(epsilon));
%si pone un limite superiore al numero
%di iterazioni, dipendente dalla accuratezza
%desiderata (epsilon) e dall'intervallo iniziale [a,b]
fa=feval(f,a); fb=feval(f,b);
for i=1:nu
   x=(a+b)/2;
   fx=feval(f,x); 
   delta=epsilon*abs((fb-fa)/(b-a));

   if abs(fx)<delta
      return
   elseif fa*fx<0
      b=x;
      fb=fx;
   else
      a=x;
      fa=fx;
   end
end
return 

>> sin (2)

ans =

   0.90929742682568

>> sin(4)

ans =

  -0.75680249530793

>> [x,nu,delta,passi]=bisez('sin',2,4,1E-15)

x =

   3.14159265358979


nu =

    51


delta =

    1.000000000000000e-015


passi =

    49

>> pi

ans =

   3.14159265358979
  

>> type fm

function y=fm(x)
y=(x-5)^5;

>> [x,nu,delta,passi]=bisez('f_e',4,7,1E-5)

x =

   6.99999427795410


nu =

    19


delta =

   0.01096626883467


passi =

    19