Metodo di Gauss-Seidel

Il metodo di Gauss-Seidel invece considera M=L+D N=-U ed ancora una volta si ha che $\det(M)\neq 0 \iff a_{i:i} \neq 0 \; \forall i$.
Lo schema del metodo di Gauss-Seidel è il seguente:

$$(L+D)x^{k+1}=(-U)x^k + b$$

e ricaviamo $x^{k+1}$ nel seguente modo

$$\sum _{j=1} ^i a_{i\:j} x_j ^{k+1} = b_i - \sum _{j=i+1} ^n a_{i\:j} x_ j ^k$$

$$\sum _{j=1} ^{i-1} a_{i\:j} x_i ^{k+1} + a_{i\:i} x_j ^{k+1} = b_i - \sum _{j=i+1} ^n a_{i\:j} x_ j ^k$$

$$x_i ^{k+1} = \frac{b_i - \sum _{j=i+1} ^n a_{i\:j} x_ j ^k - \sum _{j=1} ^{i-1} a_{i\:j} x_j ^{k+1}} {a_{i\:i}}$$

[x,passi]=GaussSeidel(A,b,$x_0$,epsilon,upper) - Data la matrice A non singolare ed il vettore $\underline{b}$ la funzione risolve il sistema lineare $A\underline{x}=\underline{b}$ mediante il metodo iterativo di Gauss-Seidel partendo dal vettore di innesco $\underline{x}_0$ con una tolleranza epsilon; la condizione per l'arresto è basata sia sul criterio del residuo, sia sul numero massimo di iterazioni upper

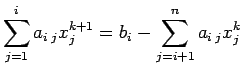
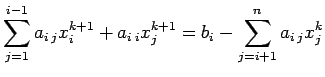
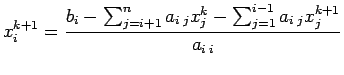
%GAUSS_SEIDEL
% function [x,passi]=Gauss_Seidel(A,b,x0,epsilon,upper)
% Pre:  A non singolare. Perche' il problema sia ben 
%	condizionato dev'essere A a diagonale dominante
%
% La function risolve il sistema lineare Ax=b con il metodo
% di Gauss Seidel.
% Riceve in x0 il vettore di innesco, in epsilon l'accuratezza
% desiderata, in  upper un limite superiore sul numero di 
% passi da eseguire.
% Restituisce in x la soluzione del sistema e in count il numero
% di passi che sono  stati effettivamente necessari per arrivare
% alla soluzione. Se passi=upper si consiglia  di riprovare con 
%un valore di upper piu' alto.
%
%See also DD, JACOBI

function [x,count]=GaussSeidel(A,b,x0,epsilon,upper)
n=length(b);
x=x0;
r=b-A*x;
count=0;
while norm(r)>=epsilon*norm(b);
    x_prec=x;
    for i=1:
        x(i)=(b(i)-A(i,i+1:n)*x(i+1:n)-A(i,1:i-1)*x(1:i-1))/A(i,i);
    end
    count=count+1;
    if ((norm(x-x_prec)<epsilon) | (count>=upper)) 
        return;
    end
    r=b-A*x;
end
return;

/tmp/cn/egausseidel.txt