Next: Metodo di Gauss-Seidel Up: Metodi iterativi Previous: Metodi iterativi Indice
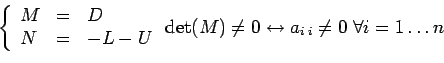
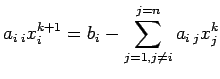
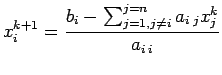
x=Jacobi(A,b,![]() ,epsilon) -
Data la matrice A non singolare ed il vettore
,epsilon) -
Data la matrice A non singolare ed il vettore
![]() la funzione
risolve il sistema lineare
la funzione
risolve il sistema lineare
![]() mediante il
metodo iterativo di
Jacobi partendo dal vettore di innesco
mediante il
metodo iterativo di
Jacobi partendo dal vettore di innesco
![]() con una tolleranza
epsilon; la condizione di arresto è basata sul metodo del
residuo.
con una tolleranza
epsilon; la condizione di arresto è basata sul metodo del
residuo.
%JACOBI
% x=Jacobi(A,b,x0,epsilon)
% Pre: A non singolare, A(i,i) non nulli per i=1:n.
% In realta' perche'il problema sia ben condizionato,
% A deve
% essere a diagonale dominante.
% La funzione restituisce in x la soluzione del sistema Ax=b,
% risolto con il metodo semiiterativo di Jacobi.
% Riceve in x0 il vettore di innesco e in epsilon la tolleranza
% desiderata.
%
% See also GAUSS_SEIDEL, DD
function x=Jacobi(A,b,x0,epsilon)
n=length(b);
x=x0;
r=b-A*x;
while norm(r)>epsilon*norm(b)
for i=1:n
som=0;
for j=1:n
if i~=j
som=som+A(i,j)*x(j);
end
end
som=(b(i)-som)/A(i,i);
x(i)=som;
end
r=b-A*x;
end
return
A =
9 6 2
3 -12 4
7 15 -3
» b
b =
1
2
4
» Jacobi(A,b,[1;2;3],1E-9)
ans =
1.00000000008960
-0.62500000007290
-2.12500000015545
» inv(A)*b
ans =
1.00000000000000
-0.62500000000000
-2.12500000000000
» A
A =
3.0000000000 1.0000000000 0.5000000000 0.8000000000
1.5000000000 9.0000000000 0.5000000000 0.6000000000
3.2000000000 4.0000000000 12.7000000000 3.2000000000
0.7000000000 3.2000000000 4.1000000000 11.3000000000
» b
b =
0.50000000000000
1.20000000000000
3.00000000000000
6.20000000000000
» inv(A)*b
ans =
-0.01092762955907
0.09772671951632
0.08447073456824
0.49102600234596
» Jacobi (A,b,[0.01;0.09;0.1;1],1E-9)
ans =
-0.01092762960712
0.09772671950406
0.08447073461875
0.49102600233408