Fattorizzazione $LDL^T$

Se una matrice è simmetrica e definita positiva allora è fattorizzabile LU, però è possibile sfruttare la proprietà di essere simmetrica per ottenere una fattorizzazione ad hoc. Sia A s.d.p. allora A=LU con

$$L= \left( \begin{array}{ccccc} 1& & & & \\ & 1& &\bigcirc &... ...ddots & & \\ & & &\ddots & \\ & & & &u_n \end{array}\right)$$

$$U= \left( \begin{array}{ccccc} u_1& & & & \\ &u_2 & &\bigci... ... & &\ddots & \\ & & & & 1 \end{array}\right) \equiv D\hat{U}$$

$A=LU$, $A=L\hat{U}=A^T=\hat{U}^T D L^T$ (D è diagonale), $LD\hat{U}=\hat{U}^T D L^{T} =A$; questa fattorizzazione è unica e implica che $L=\hat{U}^T,\: \hat{U}=L^T$ e quindi che $A=LU \rightarrow A=LDL^T$; vediamo un algoritmo efficiente per calcolare la L e la D. Dato che A è simmetrica possiamo lavorare solo sulla parte triangolare inferiore considerando solo la L e la D e non la $L^T$ quindi possiamo lavorare con gli indici i,j tale che $i\geq j$. L'elemento $a_{i\:j}$ è calcolato come $a_{i\:j}=e_i^T A e_j = e_i ^T(LDL^T)e_j = (e_i ^T L) D (L^T e_j) = (l_{i\:1} \ldots l_{i\:i}0\ldots 0) D (l_{j\:1} \ldots l_{j\:j} 0 \ldots 0 ) =$

$$= (l_{i\:1} \ldots l_{i\:i} \underbrace{0\ldots 0}_{n-i}) \l... ...ht) (l_{j\:1} \ldots l_{j\:j} \underbrace{0 \ldots 0}_{n-j}) =$$

$$= \sum _{k=1} ^{\textrm{min}(i,j)} l_{i\:k} d_k l_{j\:k} = \sum _{k=1} ^{j} l_{i\:k} d_k l_{j\:k}$$

adesso si presentano due casi

1. $i=j$
2. $i>j$

Nel primo caso

$$a_{j\:j}= \sum _{k=1} ^{j} l_{j\:k}^2 d_k = \sum _{k=1} ^{j-1} l_{j\:k}^2 d_k + l_{j\:j}^2 d_j =$$

$$= (l_{j\:j}=1) \: = \sum _{k=1} ^{j-1} l_{j\:k}^2 d_k +d_j$$

e quindi

$$d_j =a_{j\:j} - \sum _{k=1} ^{j-1} l_{j\:k}^2 d_k$$

Nel secondo caso invece

$$a_{i\:j} = \sum _{k=1} ^{j-1} l_{i\:k} d_k l_{j\:k} + l_{i\:j}+d_j + l_{j\:j}$$

ed essendo $l_{j\:j}=1$ si ha che

$$l_{i\:j} = \frac{a_{i\:j} - \sum _{k=1} ^{j-1} l_{i\:k} d_k l_{j\:k}} {d_j}$$

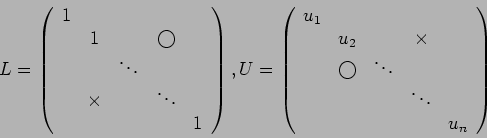
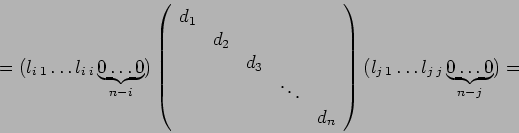
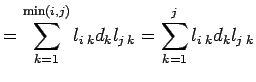
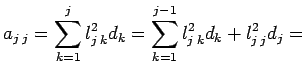
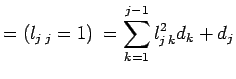
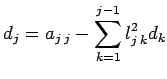
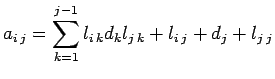
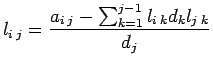
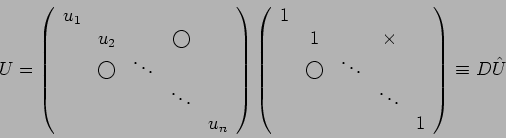
R=LD(A) - Data la matrice a non singolare e simmetrica definita positiva, la funzione esegue la fattorizzazione $LDL^{T}$ della matrice data e restituisce nella parte strettamente triangolare inferiore di R le componenti significative della matrice L, e nella diagonale restituisce la diagonale della matrice D

%LD
%R=LD(A)
%Pre: A è una matrice simmetrica definita positiva.
%
% La funzione restituisce in L una matrice che riassume 
% la fattorizzazione LDL^T di A.
% Nella parte strettamente triangolare inferiore di R si 
% trovano
  le componenti di L e la dagonale principale è 
% uguale a quella
 % della matrice diagonale D. 
% Le matrici L e D sono tali che
% A=L*D*L'
%
% See also PLU, QRHOUSE
function R=LD(A)
n=length(A);
d=zeros(n);
eta=zeros(n,n);
R=zeros(n,n);
for j=1:n-1
    som=0;
    for k=1:1:j-1
      eta(j,k)=A(j,k)*d(k);
		som=som+A(j,k)*eta(j,k);
    end
   d(j)=A(j,j)-som;
   for i=j+1:1:n
		som=0;
		for k=1:1:j-1
	    	som=som+A(i,k)*eta(j,k);
		end
	som=A(i,j)-som;
	som=som/d(j);
	A(i,j)=som;
   end
end
R=tril(A,-1);
for i=1:n
   R(i,i)=d(i);
end
return

/tmp/cn/esempio.txt