Metodo delle potenze

Supponiamo che la matrice $A$ abbia un autovalore dominante (e quindi semplice) $\lambda_1$ tale che

$$\vert\lambda_1\vert>\vert\lambda_2\vert\geq \ldots \geq \vert\lambda_n\vert$$

Il metodo delle potenze fornisce un metodo iterativo per approssimare l'autovalore dominante. Dato un vettore di innesco $u_0 \neq \underline{0}$ si definisce una successione di vettori in questo modo:

$$u_{k+1}=Au_k$$

Si può dimostrare che l'autovalore dominante è approssimato dalla seguente espressione

$$\sigma_k=\frac{u_k^* u_{k+1}}{u_k^* u_{k}} \approx \lambda_1$$

dove con $u_k^*$ si indica il trasposto coniugato del vettore $u_k$.

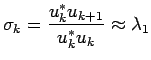
Per evitare problemi di overflow o underflow si usa una versione normalizzata del metodo delle potenze, nella quale tutti i vettori $u_k$ sono divisi per la loro norma in modo che la norma dei vettori così ottenuti sia sempre unitaria.

$$u_0 \quad \textrm{(vettore di innesco)}$$

$$y_k=\frac{u_k}{\bigr\vert \bigr\vert u_k \bigr\vert \bigr\vert _2}$$

$$u_{k+1}=Ay_k$$

$$\sigma_{k+1}=\frac{y_k^* u_{k+1}}{y_k^* y_k}=y_k^* u_{k+1}$$ (6.2)

dove l'ultima eguaglianza deriva dal fatto che $y_k^* y_k= \bigr\vert \bigr\vert y_k \bigr\vert \bigr\vert _2=1$.

La procedura Potenze utilizza lo schema (6.2) usando come condizione di arresto $\vert\lambda_k-\lambda_{k-1}\vert<\epsilon$. Nell'esempio vediamo che effettivamente trova l'autovalore dominante con una accuratezza dell'ordine di $10^{-10}$ in 12 passi e che effettivamente la soluzione trovata differisce dal risultato dato dalla funzione di libreria del Matlab eig solo a partire dalla undicesima cifra decimale e quindi il risultato è esatto fino alla decima cifra come richiesto dal nostro $\epsilon$.

[lambda,passi]=Potenze(A,y0,epsilon,upper) - Riceve in $A$ la matrice di cui si vuole calcolare l'autovalore dominante, in $y0$ un vettore di innesco (non nullo), in $\epsilon$ la accuratezza desiderata e in $upper$ un limite superiore al numero di iterazioni.
Restituisce in $\lambda$ l'approssimazione dell'autovalore dominante e in $passi$ il numero di iterazioni effettuate.

%POTENZE
%function [lambda,passi]=Potenze(A,y0,epsilon,upper)
%
% Parametri in ingresso
% A  - matrice di cui si vuole calcolare l'autovalore
%      dominante
% y0 - vettore di innesco (non nullo!)
% epsilon - tolleranza
% upper - numero massimo di iterazioni
% Restituisce in lambda l'autovalore dominante e in 
% passi il numero di iterazioni che sono state necessarie 
% per arrivare al risultato.
function [lambda,passi]=Potenze(A,y0,epsilon,upper)
y0=y0(:);
y=y0/norm(y0);
lambdap=0;
lambda=1; 
% si suppone che epsilon<1 quindi inizializzando
% in questo modo lambda e lambdap il corpo del 
% while viene sicuramente eseguito la prima volta.
passi=0;
while (abs(lambdap-lambda)>epsilon) & (passi<upper)
    yp=y;
    lambdap=lambda;
    y=A*y;
    lambda=(conj(yp)'*y)/(conj(yp)'*yp);
    y=y/norm(y);
    passi=passi+1;
end

>> A=[1 2 3 5 
4 3 2 1 
8 7 5 6
9 9 8 7]

A =

     1     2     3     5
     4     3     2     1
     8     7     5     6
     9     9     8     7


>> eig(A)

ans =

 19.41388824946578                    
 -1.55140196941206 + 0.95119045213462i
 -1.55140196941206 - 0.95119045213462i
 -0.31108431064165                    

>> [lambda,passi]=Potenze(A,[1 1 1 1],1E-10,200)

lambda =

  19.41388824945776


passi =

    12